
Distributed System Tradeoffs
Tradeoffs in distributed systems described by CAP, PACELC, Harvest & Yield
Introduction
This article takes a look at some fundamental tradeoffs in distributed systems captured by CAP, PACELC, Harvest & Yield. Let's begin with distributed systems 101 - the Two Generals Problem and FLP before jumping to the CAP Theorem. We'll finish off with an example of using CockroachDB to implement exactly-once processing semantics.
Two-Generals Problem
One thought experiment that captures the challenge with indeterminate outcomes and agreement in distributed systems, is the widely known Two Generals Problem. It shows that it’s impossible to reach an agreement between two parties if communication is asynchronous in the presence of link failures.
It goes roughly like this: Two allied armies (A and B) are on opposite sides of a fortified city in a valley, defended by army C. The two generals leading armies A and B must coordinate an attack on the city to end the siege. If either army goes in alone, they will be defeated, so a coordinated attack is required.
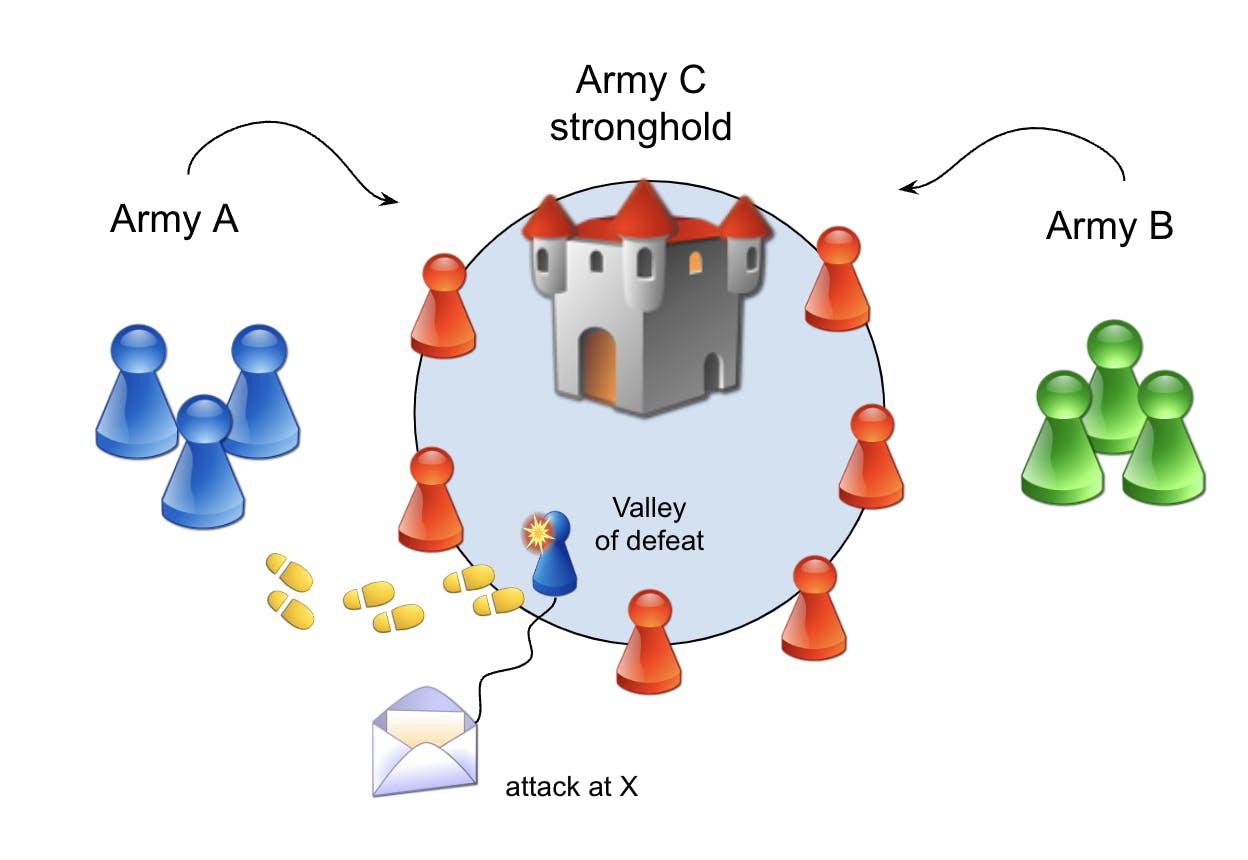
Each army general has an initial order; attack the city at some given point in time. The only way for the generals to communicate is by sending messages carried by runners through the valley, which are then prone to get captured or neutralized.
The general of army A initially agreed on communicating the time of the attack. The army A general decides on a time and dispatches a runner through the valley to carry the time of the attack to the general of army B. However, general A has no idea if the message got through or not.
Army general B decides that when the message arrives, a new runner will be sent back to acknowledge the message before attacking. But again, there's no way of telling if the reply message got through the valley or not.

(Above) One of the generals and his adjutant are on the lookout for runners.
The punch line is that it doesn't matter how many runners are dispatched from either side to solve this problem. To approach this problem militarily, both generals must accept that messages could get lost. They can mitigate that uncertainty by sending many runners instead of a single one, but it still doesn’t change the fact. Each side could send its whole army carrying the message, but the problem is still the same and it leads to the following proof:
There's no deterministic algorithm for reaching a consensus if communication is asynchronous in the presence of link failures.
Back in the binary world, a node can't determine whether another critical node for decision-making is either dead or taking too long to answer. The outcome is undetermined.
FLP Impossibility
In a paper by Fisher, Lynch, and Paterson, the authors describe what’s known as the FLP Impossibility Problem. This paper (winner of the Dijkstra award) shows that given the assumption that processing is asynchronous, and there’s no shared notion of time between processes, there exists no protocol that can guarantee consensus in bounded time in the presence of a single faulty process.
FLP is an impossibility proof that tells us that we cannot always reach a consensus in an asynchronous system in a bounded time. Specifically, FLP claims that we cannot achieve all three properties of Termination (Liveness), Agreement (Safety) and Fault Tolerance at the same time under the asynchronous network model.
That alludes that consensus is impossible, but in a practical sense by introducing the notion of synchrony and timeouts into the model (relaxation), reaching consensus is indeed possible. There wouldn’t be protocols such as Paxos, RAFT, ZAB and so forth otherwise.
Two-generals paradox and FLP are a good introduction to understanding the tradeoffs in distributed systems, leading to the infamous CAP theorem and its derivatives, or relatives.
CAP, PACELC, Harvest & Yield
The CAP conjecture, formulated by Dr. Eric Brewer, was intended to highlight tradeoffs in distributed systems. CAP is based on a simple abstraction: a single register that can hold some value that you either read (get) or write (set). When interacting with this register, the CAP theorem explicitly prohibits having both consistency (C) and availability (A) in presence of partitions (P).
It is a quite rough definition of the tensions between C, A and P in distributed systems, but it provides a useful taxonomy for highlighting these opposing forces. CAP does not model a very practical or realistic system, but that's not the point. It's more about highlighting these opposing forces and what tradeoffs that can be made.
Another, perhaps more intuitive way to put it, is that a system is either consistent or available when partitioned because partitions are not something you can choose not to have due to the network fallacies.
C, as in Consistency stands for linearizability, which is a strong consistency property where everyone read on any node returns that latest write or an error (latest referring to real wallclock time and not any causal order). This is different and not to be confused with C in ACID which stands for moving from one valid state to another valid state, preserving constraints.
A, as in Availability means total availability, where every non-failing node in the system must return a successful response but not necessarily the latest written value. Note that "must respond" is not time bound, so it’s subjective on how long that wait can be.
P, as in Partition tolerance means the system will continue to function by preserving either C or A, but never both, despite an arbitrary number of messages dropped by the network, like a network partition or split-brain scenario with multiple primaries (isolated nodes that think they are all leaders).
That is the original Brewer's conjecture which was later formally proven by Seth Gilbert and Nancy Lynch (MIT), turning it into a theorem.
Ideally, we would want both consistency and availability when partitioned, but it’s just not possible when processes are unable to share information and coordinate. Availability requires that any nonfailing node must deliver a response, while consistency requires results to be linearizable.
The bottom line is that we cannot implement a system that provides both CAP consistency and CAP availability in the presence of a network partition, and partitions are a constant we can’t ignore because our network is not always reliable.
This narrows the CAP continuum of choices to systems that are either:
Consistent and partition tolerant (C+P)
A system that prefers refusing requests over serving inconsistent data. A C+P system MUST refuse requests on all or some nodes in the event of P to preserve C.
This is the category that Google Spanner as well as CockroachDB sorts into, including most traditional SQL databases like SQL Server, Oracle, PostgreSQL etc.
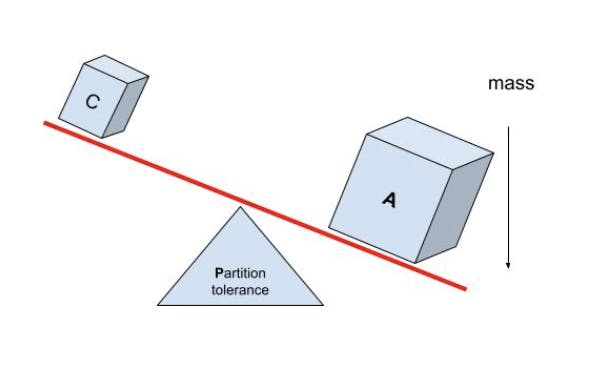
CAP is often illustrated in a triangle or a Venn diagram. Another way to look at it is that C and A are pivoting on top of P with no equilibrium*.* Either C or A will have a majority mass.
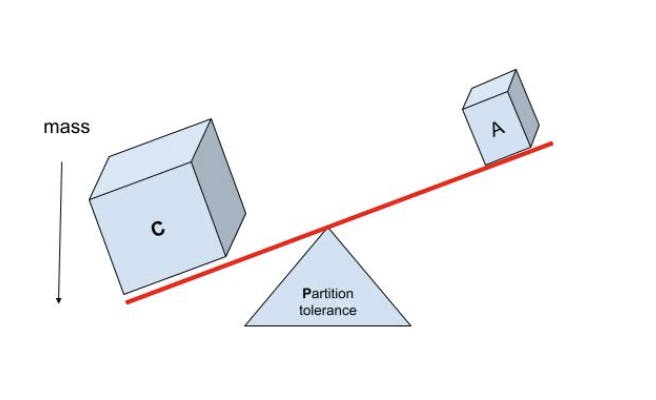
Available and partition tolerant (A+P)
A system that prefers serving potentially inconsistent data over refusing requests. An A+P system MUST respond to requests on all non-failing nodes to preserve A in the event of P, and then have to forfeit C. High availability is a separate concept (linked more to capacity) from CAP availability.
This is the category that dynamo-based systems sort into like Cassandra, DynamoDB, Riak and so on.
A “C+A” system would only mean that the system fails to provide either C or A in the presence of a partition (P) and often unpredictably. Theoretically, a C+A system would model a single node with a single wall clock and no networking (in other words, it doesn't exist).
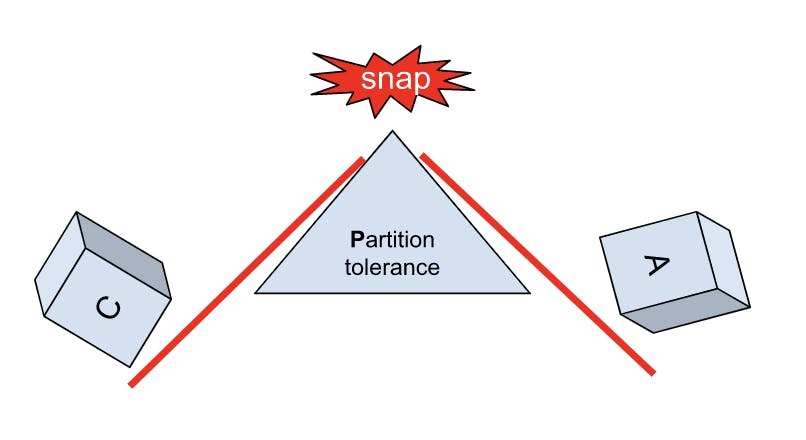
The CAP conjecture is sometimes illustrated as a triangle as if we could turn the “knobs” and have as much as we want on each of the three parameters. Balancing on the top of partition tolerance, sort of. In the meaning of the conjecture, however, we can tune by choosing between C and A but partition tolerance is not something that can be tuned or traded in any practical sense.
PACELC
The PACELC conjecture is an extension to CAP, stating that in the presence of network partitions, there’s a choice between consistency and availability (PAC). Else (E), even if the system is running in a steady state, there’s still a choice between latency and consistency (LC). It brings latency into the picture during a steady state, since unavailability is ultimately a metric of infinitely long latency.
Harvest & Yield
Harvest and Yield separate from the CAP conjecture by using more relaxed assumptions that the strict binary choices between availability and consistency.
Harvest defines the completeness of a request, let’s say you get 9 of 10 items due to a partial failure which is considered better than returning nothing.
Yield defines the ratio between the total number of attempted requests and completed ones. That way, we can trade between harvest and yield as a more relative approach.
Whether PACELC or H & Y helps to clarify the tradeoffs better than CAP, is totally up to you.
Exactly-Once Semantics
Distributed databases aren’t the only systems with strong guarantees. Messaging and streaming systems can also provide strong consistency guarantees only represented by exactly-once processing semantics. I.e if the outcome of processing an event or message is to create a permanent record with side effects, those side effects cannot be lost or turned out differently due to double-processing caused by redelivery.
Exactly once delivery at the protocol or transport level is impossible under the models described by the two-generals paradox and FLP. There are however a few methods to ensure exactly-once processing semantics in a practical sense.
One approach is to update the global state transactionally (atomically) as part of the final output from the processing. It requires that the messaging system and global state system (database) can participate in a two-phase commit protocol, which can be difficult to achieve in practice (XA/two-phase commit) since it has its own set of tradeoffs.
Another, less reliable, but still useful method without a two-phase commit is to surface business rule and data integrity conflicts early and delay the commit and message acknowledgement phase as late as possible in the business transaction. A kind of "delayed" one-phase commit. The main tradeoff is that there are no atomicity and consistency guarantees in case of transient failures in the final commit stage, which can be unacceptable depending on the business domain.
Idempotence is a third option for exactly-once processing, often used with the inbox and outbox patterns. Idempotency is a key property and is widely adopted in distributed systems design because it relieves the burden on clients to perform cleanups in case of failures. A client that doesn't receive an acknowledgement of an operation in due time (indeterminate) or a failure can simply resend the same request any number of times without causing multiple side effects (or being liable for it).
Idempotency:
Calling a function ƒ multiple times is the same as calling it once.
Multiple machines in different data centers may try to process the same event concurrently and repeatedly. That is fine, as long as all outcomes of that processing are observable exactly once in the output, which is the equivalent of exactly-once processing semantics.
In CockroachDB, uniqueness constraints are enforced globally. It provides ACID transaction guarantees and strong consistency guarantees regardless of the deployment topology, meaning also when nodes are deployed in a global manner stretching different regions or even cloud providers. That way, the database can represent a global control plane for recording side effects.
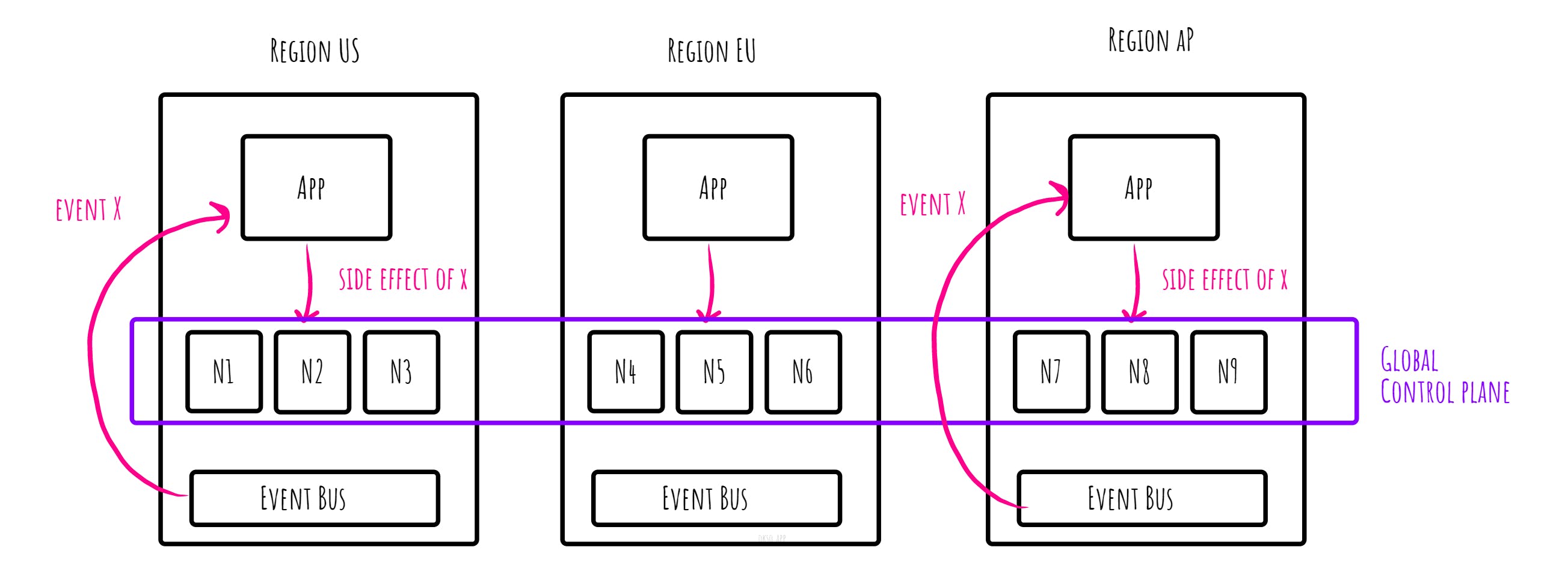
Example: A message processor writes some output and commits the outcome in a global control plane. When another processor does the same writes, based on the same deterministic input, it will have no additional effect (cancelled out).
Summary
In this article, we look at the tradeoffs in distributed systems captured by the CAP theorem and its derivatives.

